James Trimble

Network Connectivity Tracking for a Team of Unmanned Aerial Vehicles

A Dissertation Presented for the Doctor of Philosophy in Computational Engineering, The University of Tennessee at Chattanooga

James Trimble, August 2019

Abstract:

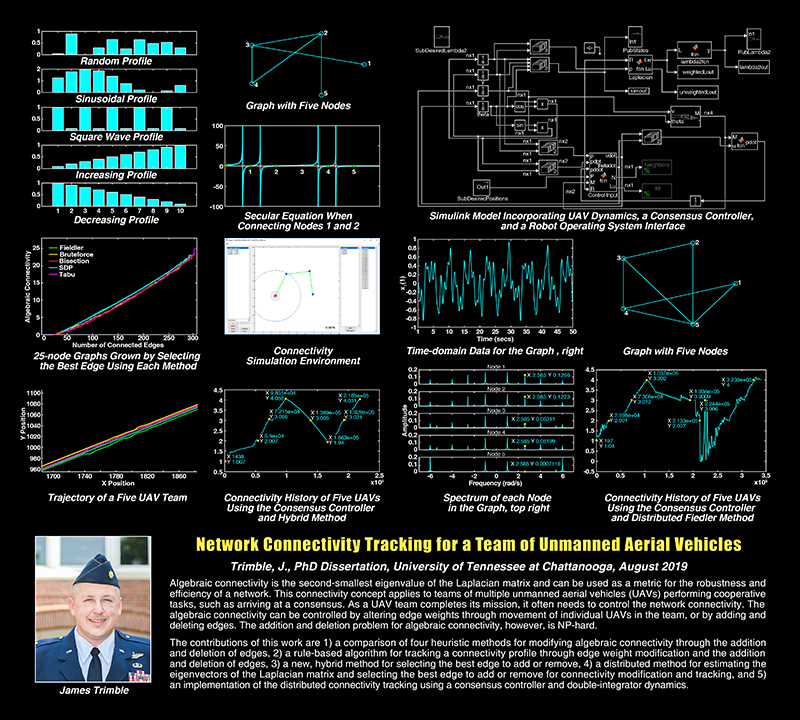
Algebraic connectivity is the second-smallest eigenvalue of the Laplacian matrix and can be used as a metric for the robustness and efficiency of a network. This connectivity concept applies to teams of multiple unmanned aerial vehicles (UAVs) performing cooperative tasks, such as arriving at a consensus. As a UAV team completes its mission, it often needs to control the network connectivity. The algebraic connectivity can be controlled by altering edge weights through movement of individual UAVs in the team, or by adding and deleting edges. The addition and deletion problem for algebraic connectivity, however, is NP-hard.

The contributions of this work are 1) a comparison of four heuristic methods for modifying algebraic connectivity through the addition and deletion of edges, 2) a rule-based algorithm for tracking a connectivity profile through edge weight modification and the addition and deletion of edges, 3) a new, hybrid method for selecting the best edge to add or remove, 4) a distributed method for estimating the eigenvectors of the Laplacian matrix and selecting the best edge to add or remove for connectivity modification and tracking, and 5) an implementation of the distributed connectivity tracking using a consensus controller and double-integrator dynamics.

Click here to access a copy of James' dissertation.