Philip Fackler
A physics-based adaptive point distribution method for computational domain discretization
A Dissertation Presented for the Doctor of Philosophy in Computational Engineering, The University of Tennessee at Chattanooga
Philip W. Fackler, December 2017
Abstract:
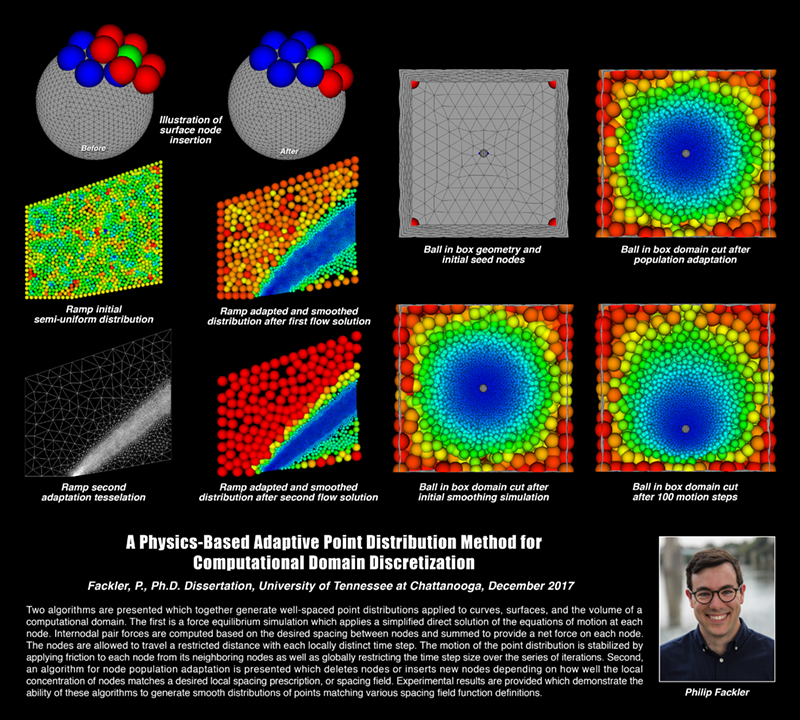
Two algorithms are presented which together generate well-spaced point distributions applied to curves, surfaces, and the volume of a computational domain. The first is a force equilibrium simulation which applies a simplified direct solution of the equations of motion at each node. Internodal pair forces are computed based on the desired spacing between nodes and summed to provide a net force on each node. The nodes are allowed to travel a restricted distance with each locally distinct time step. The motion of the point distribution is stabilized by applying friction to each node from its neighboring nodes as well as globally restricting the time step size over the series of iterations. Second, an algorithm for node population adaptation is presented which deletes nodes or inserts new nodes depending on how well the local concentration of nodes matches a desired local spacing prescription, or spacing field. Experimental results are provided which demonstrate the ability of these algorithms to generate smooth distributions of points matching various spacing field function definitions.
Click here to access a copy of Philip's dissertation.