Alma Cemerlic
Continuum Modeling of the Deceleration Transient State in Stochastic Traffic Flow
A Dissertation Presented for the Doctor of Philosophy in Computational Engineering, The University of Tennessee at Chattanooga
Alma Cemerlic, August 2015
Abstract:
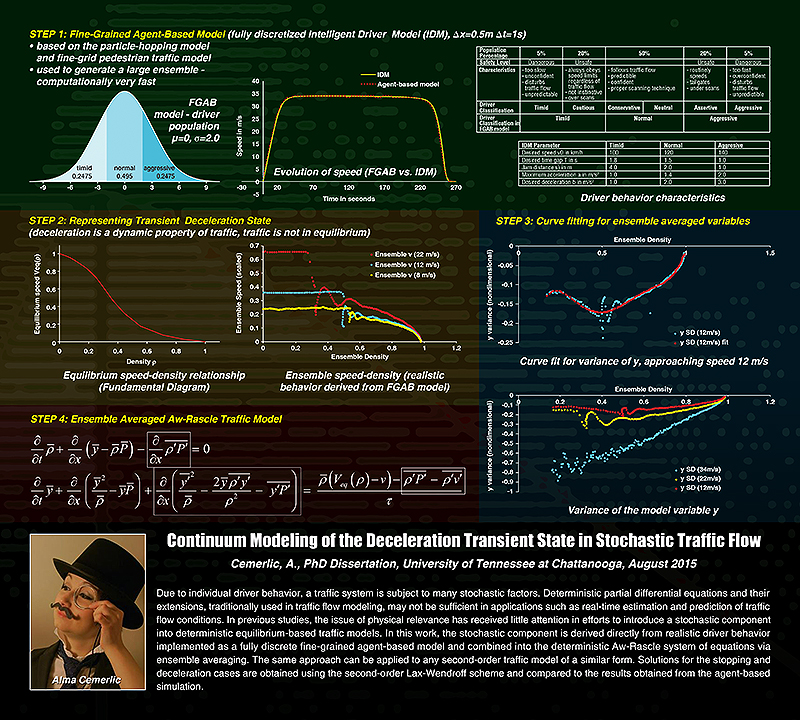
Due to individual driver behavior, a traffic system is subject to many stochastic factors. Deterministic partial differential equations and their extensions, traditionally used in traffic flow modeling, may not be sufficient in applications such as real-time estimation and prediction of traffic flow conditions. In previous studies, the issue of physical relevance has received little attention in efforts to introduce a stochastic component into deterministic equilibrium-based traffic models. In this work, the stochastic component is derived directly from realistic driver behavior implemented as a fully discrete fine-grained agent-based model and combined into the deterministic Aw-Rascle system of equations via ensemble averaging. The same approach can be applied to any second-order traffic model of a similar form. Solutions for the stopping and deceleration cases are obtained using the second-order Lax-Wendroff scheme and compared to the results obtained from the agent-based simulation.
Click here to access a copy of Alma's dissertation.