Ryan Hulguin
Direct Numerical Solution of Nonlinear Model Boltzmann Equations
A Thesis Presented for the Master of Science in Computational Engineering Degree, The University of Tennessee at Chattanooga
Ryan Hulguin, August 2008
Abstract:
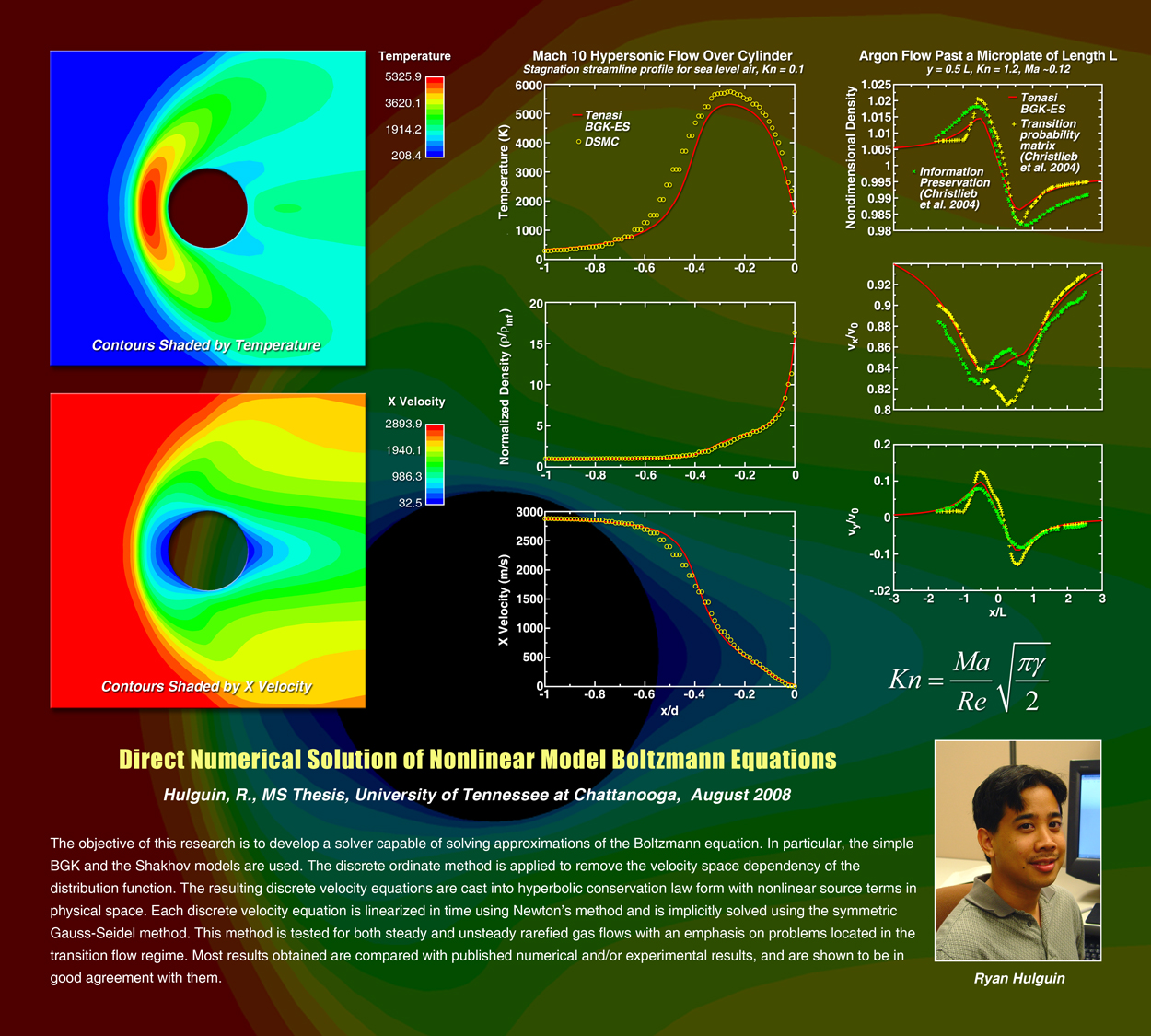
The objective of this research is to develop a solver capable of solving approximations of the Boltzmann equation. In particular, the simple BGK and the Shakhov models are used. The discrete ordinate method is applied to remove the velocity space dependency of the distribution function. The resulting discrete velocity equations are cast into hyperbolic conservation law form with nonlinear source terms in physical space. Each discrete velocity equation is linearized in time using Newton’s method and is implicitly solved using the symmetric Gauss-Seidel method. This method is tested for both steady and unsteady rarefied gas flows with an emphasis on problems located in the transition flow regime. Most results obtained are compared with published numerical and/or experimental results, and are shown to be in good agreement with them.